2018 May 8 : 最新「最難」票數: Q1-23 : Q6(10票), 16(17票), 17(7票), 21(7票)
Q24-45 : Q29(4票), 30(4票), 32(7票), 33(4票), 34(4票), 40(5票)
2018 Apr 27 : 1至10條 已加新做法,有空會再加我認為深的問題。
2018 Apr 25 : 邊條最難投票(進行中)
Q1-23 最多人投票覺得 Q6(9票), 17(11票), 21(6票)難
Q24-45 最多人投票覺得 Q29(4票), 30(3票), 32(4票), 34(3票)難
拉至頁底看「邊條最難」統計結果 及參與投票
呢年算深,頗多問題若不懂變通,便要花較多時間做。
答案
1-10 BDCAA DDCDB
11-20 DACBD ABBDB
21-30 CBBAD CCACA
31-40 CCDCB ADBBA
41-45 DACBA
有問題(或有好方法)請留言。
**謝謝 Eddy Tsang 對第17條的方法分享 (2018 Apr 16)
~~~ 2018 年經濟 MC 逐題解釋 ~~~
~~~ ~~~ ~~~ ~~~ ~~~ ~~~
Q1-23在此 | Q24-45 詳細答案在下方
~~~ 題號下方標記意思 ~~~
*sub - 可代數試 | *mc - 有 MC片教(youtube)
*skl - 有特別MC技巧 | *fmla - 有計數機內置程式可用
*prg - 有計數機程式可用 | *cal - 有等別計數機用法
∴ the locus of P must have same slope: A, B 錯
L1 × 8 : 24x − 8y + 56 = 0
L2 × 2 : 24x − 8y − 22 = 0
centre: (3, -1)
radius: √(3² + 1² - 1.2) = √88
計完 radius 應 check C 先,∴ √88 ≈ 3
C: circumference: 2 π (3) ≈ 18.8 < 20 ✓
A: √((3 - 0)² + (-1 -0)²) = √10 > √88 ∴ lie outside ✗
B: ∵ centre x-coordinate = 3 → radius < 3
∴ cannot lie on QII ✗
&=P(1\cap&space;4)+P(2\cap&space;3)\\&space;&=P(14)+P(41)+P(23)+P(32)\\&space;&=\frac{3}{7}\times\frac{1}{6}\times2+\frac{2}{7}\times\frac{1}{6}\times2\\&space;&=\frac{1}{7}+\frac{2}{21}\\&space;&=\frac{5}{21}&space;\end{align*})
Alternative method
1, 4 組合 3 款;2, 3 組合 2 款
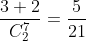
x = 168
32. C
*skl
(以 y = x 為對稱軸,把曲線反過去便是 log 的 基本圖 a > 0)
I ✓ 記住基本 exp. function [ y=ax ] 既圖(左向右升)
II ✗ (從答案選項知 I ✓ 則 II ✗ )
亦可以基本exp. fn 反射去諗,若把 y = log b x,所以 b > a
III ✓
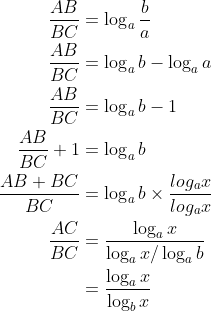 ∴ Ans = 9
∴ Ans = 9
*sub - 可代數試 | *mc - 有 MC片教(youtube)
*skl - 有特別MC技巧 | *fmla - 有計數機內置程式可用
*prg - 有計數機程式可用 | *cal - 有等別計數機用法
~~~ ~~~
24. A *skl (秒殺題)
∵ ∠COD = ∠DOE = 90°
∴ CD = 20 (∵ 3-4-5 )
∴ DE = 13 (∵ 5-12-13 )
∴ perimeter = 13 + 20 + 5 + 16 = 54
∴ CD = 20 (∵ 3-4-5 )
∴ DE = 13 (∵ 5-12-13 )
∴ perimeter = 13 + 20 + 5 + 16 = 54
5*技巧 : 畢氏定理靚比例: 3-4-5; 5-12-13 (Q1-23 已經用左 3 條啦)
5*技巧 : 做座標題最好最好畫出黎 !!! 易做好多 !
25. D *skl
notice that L1 & L2 have same slope : -3/-1 = -12/-4 = 3∴ the locus of P must have same slope: A, B 錯
L1 × 8 : 24x − 8y + 56 = 0
L2 × 2 : 24x − 8y − 22 = 0
the eqn of locus : 24x − 8y + C = 0
where C = (56 + (-22)) ÷ 2 = 17 (∵ equal distance)
where C = (56 + (-22)) ÷ 2 = 17 (∵ equal distance)
26. C *skl
➀ 學 plot 圖:slope = -4/3
y-intercept : put x = 0 ⇒ y = 12
x-intercept : put y = 0 ⇒ x = 9
➁ ∵L2 ⊥ L1
∴ slope of L2 = -1 ÷ (-4/3) = 3/4
用 slope 3/4 的意思 Δy/Δx = 3/4
∴ L2 的 x-intercept = 12 × 4/3 = 16 (負)
➂ Area: [9 - (-16)] × 12 ÷ 2 = 150
y-intercept : put x = 0 ⇒ y = 12
x-intercept : put y = 0 ⇒ x = 9
➁ ∵L2 ⊥ L1
∴ slope of L2 = -1 ÷ (-4/3) = 3/4
用 slope 3/4 的意思 Δy/Δx = 3/4
∴ L2 的 x-intercept = 12 × 4/3 = 16 (負)
➂ Area: [9 - (-16)] × 12 ÷ 2 = 150
27. C
C: x² + y² - 6x + 2y + 1.2 = 0centre: (3, -1)
radius: √(3² + 1² - 1.2) = √88
計完 radius 應 check C 先,∴ √88 ≈ 3
C: circumference: 2 π (3) ≈ 18.8 < 20 ✓
A: √((3 - 0)² + (-1 -0)²) = √10 > √88 ∴ lie outside ✗
B: ∵ centre x-coordinate = 3 → radius < 3
∴ cannot lie on QII ✗
28. A
Alternative method
1, 4 組合 3 款;2, 3 組合 2 款
29. C
(6 × 108 + 4 × x) ÷ 10 = 132x = 168
30. A
➀ Q1 = 30 + a
Q3 = 60 + b
➁ 當 Q3 = 60, Q1 ≥ 35(要 IQR ≤ 25)
由此排出 b 在不同數時,a 的可能數值
| b | | | a | ||||
| 0 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 6 | 7 | 8 | 9 | ||
| 2 | 7 | 8 | 9 | |||
| 3 | 8 | 9 | ||||
| 4 | 0 |
當Q3 = 65 → Q1 ≥ 40,已超出 ‘3’ 的 stem
∴ I, II ✓
III:上表等一列已顯示 a - b 可以等於 5, 6, 7, 8, 9 ✗
31. C *skl
明顯兩圖像有
上下倒轉
及
左右平移
; g(x) = f(x+a)
明顯兩圖像有
上下倒轉
及
左右平移
; g(x) = f(x+a)
32. C
*skl
(以 y = x 為對稱軸,把曲線反過去便是 log 的 基本圖 a > 0)
I ✓ 記住基本 exp. function [ y=ax ] 既圖(左向右升)
II ✗ (從答案選項知 I ✓ 則 II ✗ )
亦可以基本exp. fn 反射去諗,若把 y = log b x,所以 b > a
III ✓
33. D
Using 2 points:
m = (6 - 2) / (9 - 1) = 1/2
c = 3/2
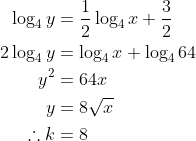
Alternative method
y = kxa
Using 2 points:
m = (6 - 2) / (9 - 1) = 1/2
c = 3/2
Alternative method
y = kxa
log4y = log4k + alog4x
(1,2): 2 = log4k + a — ➀
(9,6): 6 = log4k + 9a — ➁
➁−➀: 8a = 4
a = 1/2
From ➀: 2 = log4k + 1/2
log4k = 3/2
√(4³) = k
k = 8
34. C
*skl
➀ Draw 4 eqn in the system (slope be on-scale)
➁ Shade the section
➂ Draw 5x + 6y = 0
(notice that slope -5/6 be less steep than -3/2)
➃ Notice move it to left make 5x + 6y smaller, so find pt. A to be the least value pt.
➄ x - y = 35 ⇒ x = 35 + y —➀
Sub ➀ into 3x + 2y = 0
3 (35 + y) + 2y = 0
105 + 5y = 0
y = -21
x = 14
∴ 5x + 6y + 234 = 5(14) + 6(-21) + 234 = 178
*skl
➀ Draw 4 eqn in the system (slope be on-scale)
➁ Shade the section
➂ Draw 5x + 6y = 0
(notice that slope -5/6 be less steep than -3/2)
➃ Notice move it to left make 5x + 6y smaller, so find pt. A to be the least value pt.
➄ x - y = 35 ⇒ x = 35 + y —➀
Sub ➀ into 3x + 2y = 0
3 (35 + y) + 2y = 0
105 + 5y = 0
y = -21
x = 14
∴ 5x + 6y + 234 = 5(14) + 6(-21) + 234 = 178
35. B
[Notice it’s the sum]
➀ Sub n = 1 ⇒ 6(1)² − (1) = 5
⇒ II ✓
➁ Sub n = 2 ⇒ S(2) = 6(2)² − (2) = 22
n = 3 ⇒ S(3) = 6(3)² − (3) = 51
∴ T(1) = 5
T(2) = S(2) - S(1) = 22-5 = 17
T(3) = S(3) - S(2) = 51-22 = 29
⇒ I ✗
➂
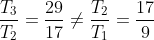
⇒ III ✗
[Notice it’s the sum]
➀ Sub n = 1 ⇒ 6(1)² − (1) = 5
⇒ II ✓
➁ Sub n = 2 ⇒ S(2) = 6(2)² − (2) = 22
n = 3 ⇒ S(3) = 6(3)² − (3) = 51
∴ T(1) = 5
T(2) = S(2) - S(1) = 22-5 = 17
T(3) = S(3) - S(2) = 51-22 = 29
⇒ I ✗
➂
⇒ III ✗
36. A
2m² + 5m - 14 = 0
2n² + 5n - 14 = 0
∵ same function
∴ it’s quaduatic
∴ m + n = -5/2
mn = -14/2 = -7
∴ (m+2)(n+2)
= mn + 2(m + n) + 4
= -7 + 2(-5/2) +4 = -8
37. D
2m² + 5m - 14 = 0
2n² + 5n - 14 = 0
∵ same function
∴ it’s quaduatic
∴ m + n = -5/2
mn = -14/2 = -7
∴ (m+2)(n+2)
= mn + 2(m + n) + 4
= -7 + 2(-5/2) +4 = -8
37. D
*cal *skl
記 i 每 4 次方可消
Use Calculator CMPLX mode
+5(-i)+6}{1-i}=&space;3+i)
Alternative methodi12 可直接入機:i223 (i) (x²)(x²)(x³) 次序可轉,即{[(i)²]²}³
38. B
(\cos&space;x-1)&=0\\&space;\cos&space;x=-\frac{5}{6}&\textup{&space;OR&space;}&space;&\cos&space;x=1\\&space;\Rightarrow&space;\textup{2&space;roots&space;}&&\Rightarrow&space;x=0^{\circ}\\&space;&&\Rightarrow&space;\textup{1&space;root}&space;\end{align*})
∴ 3 roots
39. B
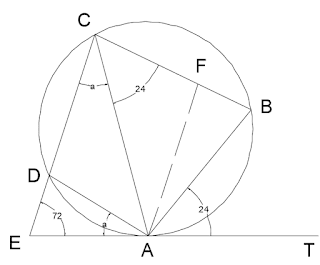
見圓加 tangent
∠ACB = 24° (∠ in alt segment)
Let a be ∠DAE,
∠DCA = a (∠ in alt segment)
∠ADC = a + 72° (ext. ∠ of Δ)
Draw AF//DC
∠AFB = ∠DCB = a + 24° (base ∠s, isos Δ)
∴ a + 24° + a + 72° = 180° (cyclic quad.)
∴ a=42°
∴ ∠ABC = 42° + 24° = 66°
40. A
*skl
由於由 P 垂直的高是 PO,
∴ orthocentre 為 (10, 0)
m of PQ = -2/5
∴ m of RS = (-1) ÷ (-2/5) = 5/2
用 slope 定義理解 5/2 即向右行 2 格
便升 5 格
∴ y = -25
Alternative method
設 R (0, y)
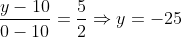
41. D
*skl
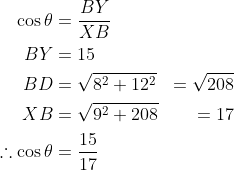
42. A
43. C
*skl
&space;&=P(%276%27)+P(%272345%27\cap&space;%272345%27\cap&space;%276%27)\\&space;&+P(%272345%27\cap&space;%272345%27\cap%272345%27\cap&space;%272345%27\cap&space;%276%27)+...\\&space;&=\frac{1}{6}+(\frac{4}{6})^{2}(\frac{1}{6})+(\frac{4}{6})^{4}(\frac{1}{6})+...\\&space;&=\frac{\frac{1}{6}}{1-(\frac{4}{6})^{2}}\\&space;&=\frac{3}{10}&space;\end{align*})
Alternative method
諗:John 擲先,起碼有 1/6 機會有 '6',而即使佢第一擲唔得,之後都有機會再擲出 '6'
所以答案應該比 1/6 大少少,所以選 C
44. B
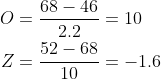
45. A
A.S. means they are having common difference.
記 i 每 4 次方可消
| i | = | i | ||
| i² | = | -1 | ||
| i³ | = | (-1)(i) | = | -i |
| i4 | = | (-1)(-1) | = | 1 |
| i5 | = | (1)(i) | = | i |
Use Calculator CMPLX mode
i13入:i223 i (i)(x²)(x²)(x³)(i)
38. B
∴ 3 roots
39. B
見圓加 tangent
∠ACB = 24° (∠ in alt segment)
Let a be ∠DAE,
∠DCA = a (∠ in alt segment)
∠ADC = a + 72° (ext. ∠ of Δ)
Draw AF//DC
∠AFB = ∠DCB = a + 24° (base ∠s, isos Δ)
∴ a + 24° + a + 72° = 180° (cyclic quad.)
∴ a=42°
∴ ∠ABC = 42° + 24° = 66°
40. A
*skl
由於由 P 垂直的高是 PO,
∴ orthocentre 為 (10, 0)
m of PQ = -2/5
∴ m of RS = (-1) ÷ (-2/5) = 5/2
用 slope 定義理解 5/2 即向右行 2 格
便升 5 格
∴ y = -25
Alternative method
設 R (0, y)
41. D
*skl
42. A
43. C
*skl
Alternative method
諗:John 擲先,起碼有 1/6 機會有 '6',而即使佢第一擲唔得,之後都有機會再擲出 '6'
所以答案應該比 1/6 大少少,所以選 C
44. B
45. A
A.S. means they are having common difference.
Q1-23在此
2018 DSE Math MC 你覺得邊條最難?(Q24-45)
參與投票 |
若覺得這篇文章好,"分享" 給朋友吧!或留個 "Thank You" 呀!
想收到最新文章,可訂閱博客更新。
[keep updating (列出相似題目比讀者做, 列秒殺題)]











沒有留言:
張貼留言
若想 *收到回覆* 通知,請以 Google 帳號登入,並勾選「通知我」(你依然可選擇 *匿名(唔開名)*) 。
另,Google 偶會審核留言而不能即時顯示,請耐心等候,不用重覆發表。謝謝!