2012-2017 HKDSE Math 歷屆數學不同級別(Grade)所需分數 cut off 及其分析

本文目的：

1. 坊間 cut-off 出處係邊？準嗎？
2. 啲 cut-off 原貎(原始數據)係點？
3. 真實 cut-off 係幾多？
4. 啲 cut-off 數據，有否反映出其他資訊(如考卷深淺變化)？

本文希望能為此提供答案。（如有問題請留言）

(一) 坊間 Cut-off 來源：某大討論區

網上所有 Cutoff 資料，其實全出自某學生討論區，佢地每年都收集分數 (覆卷考生無私交出 check 卷結果)，再整理 得出大約既 Grading 分數*，使莘莘學子得益。
(*係大約咋，下文會講點解係大約，同應該點用呢啲數據)

(點解考試局唔公開呢啲資料呢？好多外國公開試都有咁做。)
(唔唔，應該係，除非唔係。)

咁有用既資訊，自然會傳呀～傳呀～

但係，轉載呢啲 cut-off 分既人，全部都當佢係 "真正" 既 cut-off (疏忽，定無知？)。呢啲咁求求其其既態度，做學問最錯既地方莫過於此！(在我補習生涯，見數渣通常就係呢種態度...)

本文目的，希望同學及家長可以客觀啲、準確去理解啲 cutoff 資料。

相關文章：『 DSE 卷一卷二佔分比重拉Curve？』

經過一番功夫，我把所有原始數據整理好，做左下面的試算表：

(二) 2012-16 Math Cut-off 數據概要表 (Summary)

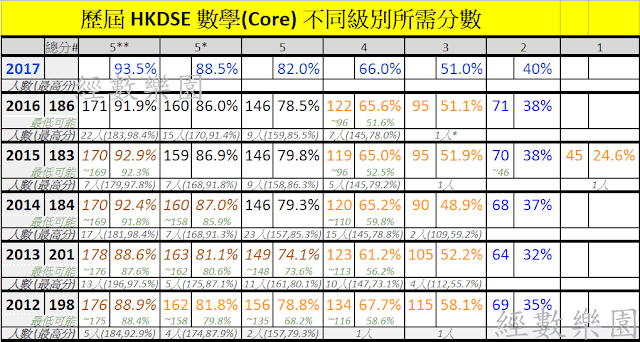圖1：12-16年 Math Cut-off 數據概要表

注1：2017 年 Cut-off 為估計值，按本年試題程度調整，今年程度稍淺，估計 cutoff 分數應比往年提高少少。
注2：計攞幾多％ = (卷1估計得分/105)x0.63 + (卷2估計啱題數/45)x0.37 [點解唔係65/35比請看此文]
注3：以上圖表點用點解讀請詳閱本文

(三) Cut-off 數據概要表使用方法

3.1) 每一儲存格代表意思：

3.2) 不同顏色表示 cutoff (分, %) 的確定程度：

3.3) 以 13 年為例，詳解儲存格意思：

(四) Cut-off 概要表基本觀察 (12-16年)

4.1) 只有 6 個 100%肯定的 Cut-off 分

• 圖中紅圈內黑字係肯定的 Cutoff 分，只有6個。
• 分別係 2016 年 5**, 5* , 5，2015年既 5*, 5，同埋2014年既 5。 
• 例如，2016年我有171分(91.9%)，就有5**啦（咁17年或之後要幾分呢？文章稍後會再分析）

點解呢6個係肯定呢？
因為該級別的最低總分，只比低一級別的最高總分，高1分。所以若你攞少呢1分，就低1個 grade。 

171、160 呢啲總分點得黎？
簡單講，係評卷記錄先有既，每年唔同（見圖，尾二個行[紅圈 out of 183]）
[詳可見『數學 Paper 1 佔 65％，Paper 2 佔 35％？』]

4.2) 大多級別報分人數不足

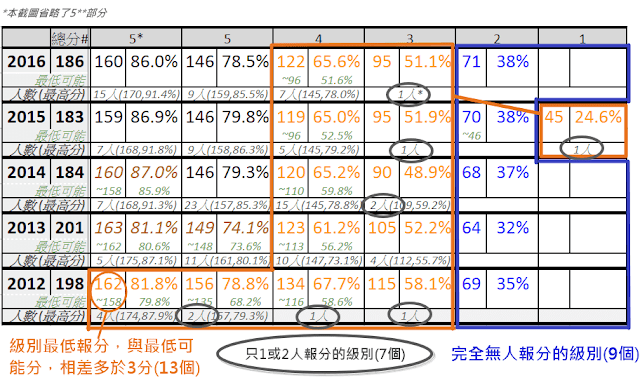
• 完全無人報分的級別，有9個 (級別1及2)；
• 只有1人或2人報分的級別，有7個 (主要是級別3)；
• 級別最低報分，與最低可能分，相差多於3分(13個)

以上這些級別的 Cut-off，基本上要靠估。

其實，都可以估得有譜啲既。

(五) 估計2017年(及之後) 的 Cutoff 

5.1) 假設

估計 2017年及以後既 Cut-off 大約會跟 2014-2016 的％；因為首兩屆文憑試(2012及2013) cut-off，同隨後3年之相差頗大。估計頭兩年 HKEA 出卷水平可能調整中，之後逐漸隱定下來 。

5.2) 首兩屆 DSE 與之後三屆 的 Cut-off 比較

• 下表表示在兩段年期間，成績最少及最多需要幾多百分比，便可穩獲某級別。
• 例如在 14-16年間，最少 91.8，最多 92.9%，就必定夠攞 5**

	14-16年	(中間值)		12-13年	(中間值)
5**	91.8-92.9%	92.4%		(88.4-88.9%)	88.7%
5*	85.9-87.0%	86.5%		(79.8-81.8%)	80.8%
5	78.5-79.8%	79.2%		(68.2-78.8%)	73.5%
4	51.6-65.6%	58.6%		(56.2-67.7%)	62.0%

注1：上表數字是按圖1(數據概要表)抽出最高報分的％，及最低可能％(低一級別最高分+1，再轉％)
注2：中間值＝(最大值+最小值) ÷2
注3：橙色字 表示範圍較大，高低相差多於 3% (其實都可以推算，下文會講)
注4：級別 3,2,1 近乎完全沒有人報，不能估計結果

5.3) 5**, 5*, 5 級別 的 Cut-Off (非常肯定 [誤差 < ±1%])

從上表看出以上三個級別14-16年的所需分數，幅度極少，最多只有 1.3% (級別5)。
除非份卷極淺(應該唔多會發生)(17年算淺)，如果唔係以上 % 唔可能差太遠。

估計 2017 年及往後數年：

• 攞93%，穩攞5**
• 攞87%，穩攞5*
• 攞80%，穩攞5

5.4) 級別 4 的 Cut-Off (推算，頗準 [誤差 < ±3%])

級別 4 的 Cut-off 較不精確，因級別 3 的報分人極少，12-16 五年間只有9人 (平均每年只有 1.8人) [因為要以級別 3 的最高分，去決定級別 4 的 cut-off ]。

但幸運的是，在 13 及 14 年度的報分者裏：

• 級別 4 足夠多 (分別 10、15人)；
• 級別 3 的分差夠大 (14 年分差達 18 分)，應接近該組別之全距 (Range) (最大值減最小值)

我用了一些數學方法，推算出14-16年真正 Cut-off，平均約為 62.5%。

~ 推算過程如下(無興趣者可直接跳過) ~

步驟1) 初步估計分數 (只看 13, 14年的級別 3 及 4 報分)

在13年，

• 10人報分為級別4，最低分123，最高分147； 
• 4人報分為級別3，最低分105，最高分112 (即 cutoff = 112 + 1 = 113)； 
• 實際 cut-off 應在 113-123 之間 

• 級別 4 的報分者較多，因此估計 123 分會較近 cut-off； 
• 級別 3 的報分者較少，因此估計 113 分與 cut-off 應差較遠； 
• 用中三的 Co-ordinate Geometry 的 Section Formula (坐標幾何 的 分點公式) 估計 cutoff：

  [123 × (4 × 1.5*) + 113^ × 10] / (4 × 1.5 + 10) = 116.75 → 117 (58.2% --- (1))

(*因級別 3 的分數分佈應比 4 的更濶，所以 ×1.5 以增加其比重)
(^用113因為 112 分只可攞 3)

在14年，

• 同樣方式，估計分數為：

[120 × (2 × 1.5) + 110 × 15] / (2 × 1.5 + 15) = 111.7 → 112 (60.9% --- (2))

步驟2) 按其他已知資料調準分數(參考其他級別兩年間差異) 

以(2)減(1)，13至14年的初步 cutoff，上升了 2.7%。
但同期其他級別上升較多，5* 及 5 皆升約 5.65% (中值)；

以此推算(5*, 5 及 4 應較類近)，若要將 (1), (2) 兩個 % 加濶至相差 5.65%，則 (2) 要變成 62.475%；(1) 要變成 56.725%  (分別加及減 1.475)

~ 推算過程完 ~

---

5.5) 級別 3 的 Cut-Off (估計，不準 [誤差 > ±3%])

要估計級別3，只可用2013及2014年的數據，其餘年份皆只有1人報分。

13年雖然有4人報分，但分數太近，只差7分；
相反，14年只有2人報分，但

• 兩人分數差19分
• 已經好近40%左右的合格分數

所以當年90分(48.9%) 應好接近級別3的 cutoff，因得兩個數據所以真正 cutoff 好可能會再低一點，如 47.5%

(六) 2013年考卷出得較深

在 12-16年 cutoff 數據中，還觀察到另一現象，便是2013年 cutoff 是歷屆最低的，即考卷出得較深 (所以 cutoff 定低一點，讓多啲同學去到該級別)。雖然 cut-off 唔夠肯定，但該年級別 5**, 5*, 5 的 cutoff 都頗精確，但都是歷屆最低%。所以以上推論應該無誤。

(七) 2017年預計數學科級別 Cut off 成績

2017年偏淺，但非極淺。我估cut-off 最盡如下(最盡即好穩陣)：

5**(93.5%), 5*(88.5%), 5(82.0%), 4(66%), 3(51%), 2(40%)


如有任何問題請留言。

若覺得這篇文章好，"分享" 給朋友吧！或留個 "Thank You" 呀！
想問經濟、數學？可 按此 到我的面書發問。
想第一時間收到最新文章，可訂閱博客更新 / RSS 。