最近又有數個學生有這問題, 所以整理左一些對應練習給他們:
(17張圖片 | 亦可 下載 pdf)
要求: 1) 不計出原數(i.e, 100%) 前提下嘗試計出答案,
2) 不用計數機(可用算草) ;
3) 盡量試諗最快捷方法
目的: 強化乘除/倍數/心算/分數概念
以第一張圖作例子, 可以試用倍大/縮小 (或比率原理)方法計出答案, 舉例:
1) 25% 為 17英磅 , 50% 為 25% 的兩倍, 所以為 17 x 2 = 34 英磅。
9) 150 英磅 為 60 英磅的 2.5倍, 10% 的 2.5 倍 (2倍再加 0.5份) 為 25%。
1) £34, £70, £60, £300, £150, 100; 6) £30, 10, 25, £18, 30, 80;
13) 100, £18*, 25*, 5*, 72, 10; 19) 80, £27*, 25*, 33*, 55*, 36*
14) 1/3 is £20, 1/30 is £2, 30% = 33⅓% - 3⅓%;
15) find 10% first;
16) see 4.5 is half of 9; 10% = £9 ;
20) 6⅔ = £12, so 60% = 120 - 12 = 108, 15% = 108 ÷ 4
20) see Q14 method
21) method 1: try simplify 40/128 ; method 2: 40% = £64 ; 20% = £32
22) see Q21
23) find 10% is ? first
24) find 30% is ? first
部分做法參考:
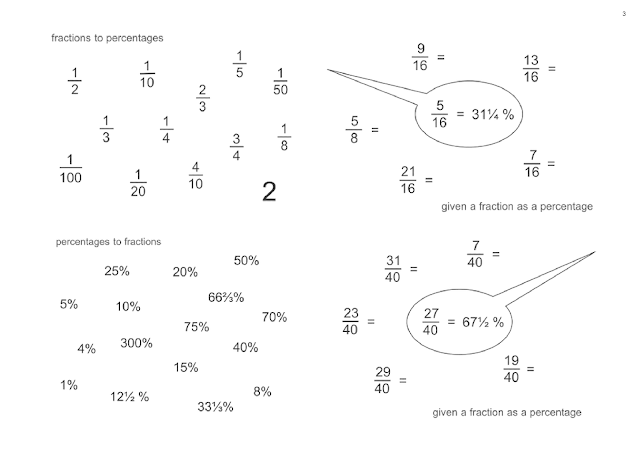
頁3(右上,右下) 13/16 = 5/16 + 50 = 81¼% ; 5/8 = 5/16 x 2 = 62½%
頁5上行左2, 下行左1的圖: 看對稱性 ; 其他: 計算正方形面積, 或可合併作一長方形
頁6-7: 與頁3 右上右下同類
頁8右側答案: 1)13/20, 13/20, 13/50, 13/65, 16/20, 16/50, 21/35, 21/60, 31/50, 31/62 ; 2)36/48, 36/75, 63/75, 63/84 ; 3) 79/80 = 98.75%
頁9左下: 先計 6¼% = 5 + 1¼%; 6¼ = 2 x 3⅛ ; (右側)分子非1 的3條, 可照樣分拆: 31¼ = 25 + 6¼ (或者做熟可能會睇到: 6¼ x 5 = 31¼)
頁9右下: 可以 ⅓ 的小數值去解 (5), (8), (9); (10)可以 25% 去諗