[香港] 會諞人的統計數字，結構性赤字？選不同起點有完全相反結果

較早前公報了《長遠財政計劃工作小組報告》，引來不少爭議，其中一項爭議是認為《報告》按不同假設，推算最快7年會出現結構性財赤。事實是否真的這樣呢? 當然不是。

我整理了 無線 新聞透視 的報導:

最簡單講，何時作起點的結果有著絶對性的影響！！！買股票睇圖表五十天線，二百五十天線講既野都唔同啦！

(以下引述自雷鼎鳴教授博客)

以1997年作起點年，頗有不妥，若是用其他年份作起點，例如1992（黃元山）、1998（羅致光）及2008（徐家健），結果便十分不同。
政府內部作推算時曾以80年代中作起點，結果分別不大，
但上述諸君皆非胡言亂語之人，為何用他們的起點年份會造成不同的結果呢？他們的觀點倒促使我再次詳細檢閱數據，終有兩點體會。

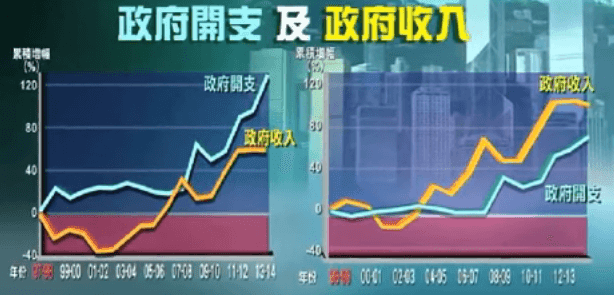
第一(RC:三次年度大幅增長扭曲趨勢)，政府開支並非年年跑贏GDP，在很多年份GDP增長都快於開支增長。但在91至93、98及08三段時間內，開支都大幅拋離GDP，91至93的一次，開支增幅減GDP增幅等於25％，98年是28％，08年是31％，就是這三次，開支累積增幅才遠大於經濟增幅。若以這些年份作起點，便等於忽略了最關鍵的增長年份，所以才會得到與《報告》不同的結果。這有如二人賽跑，甲只有三段時間發力狂衝，把乙拋離，其餘的時間甲的速度都與乙差不多，甚至更慢，我們若忽視了這三段衝刺時段，便不能明白為何甲會勝出。  (RC: 這與計算買入資產(如買樓)的複式回報率一樣，買入時機很重要。若你在97年樓價最高時買入，或在2000年(已跌了一大截)買入，然後一直持有至現在，你的回報率會截然不同。所以選擇年期不同當然會有不同的推演結果。若你想有筆錢想投資，想知買樓的回報，經紀就假設你在2003年(樓價最低)時買入去計年回報率給你，回報率自然會很高。但試問，你可能每次投資都可把握到最低位買入嗎? 所以教授這裏的原因實在非常有力)

第二(RC: 政策改變使結構性變周期性)，在檢查數據中，我倒是發現在過去，政府開支與GDP的關係頗有波動。這便帶來一個重要問題，究竟現在可預見的赤字是結構性（亦即持續性不易逆轉的）還是周期性。例如，在2001至04年間，政府開支很大，但後來被各種緊縮政策打了下去，政府當時本來是擔心有結構性赤字的，但終因其努力而把赤字從結構性改為周期性。未來會否歷史重演？這會比從前困難得多，因為未來造成財赤的一大動力是人口老化，而人口老化絕對不是周期性而是長期性的。此外，香港事事都已變得政治化，要政府控制開支的增長是政治上不討好之事，政治因素或已成為結構性問題了，財赤也結構性的機會大增。
日本本來也是一個懂得量入為出，人民有高儲蓄率的國家，但縱使在此種國家，在人口老化的壓力下，政府開支一樣從二十多年前佔GDP的30％上升至今天佔40％，但大家都不願加稅，所以收入維持在GDP的30％不變，香港人口老化比日本晚了大約15年，日本的經驗豈能不察？