[老師不教的數學] 畢氏定理(Pythagorean theorem) 的証明？GIF動圖詳解。[中二識用, 小五可試]

 -- 本文較多動圖(gif)，載入可能需較長時間 --

畢氏定理 (不是定理! )，一條你中學必學的公式：

直角三角形的兩條直邊平方相加＝其斜邊的平方

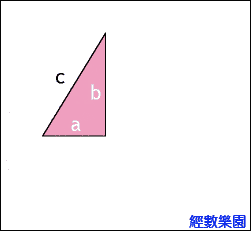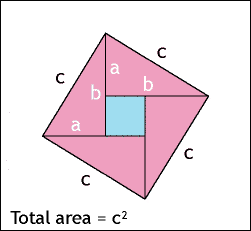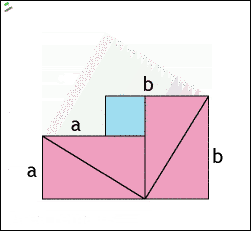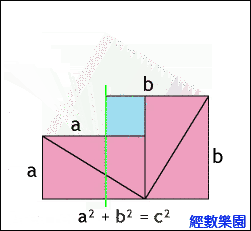
1. 兩個小正方形(直邊) 剛好可注滿大正方形(斜邊)的水

2. 斜邊畫正方形補滿 再扣減相同面積

1. 以一直角三角形(黃色) 的斜邊邊長畫一 正方形(紅色)
2. 加多 3 個 黃色直角三角形，形成一大正方形。
3. 複製一個至右邊 
4. 右邊把 4 個 黃色直角三角形 合拼作兩個長方形 (注意大正方形的總面積[紅+黃]相等)
5. 左/右兩邊一起扣掉其中三個 黃色直角三角形 (餘下面積依然相等)
6. ⬛ +◢  = ◢ + ◾ + ◼     ⇒     ∴⬛(紅) = ◾(藍) + ◼(綠)

3. 四個直角三角形圍出大正方形 平移變兩個較小正方形 

1. 一直角三角形(粉紅色)，把其旋轉複製，以其斜邊作一長為 c 的正方形(面積:粉紅+淺藍)。
2. 把上方兩個直角三角形移向底，形成兩個邊長分別為 a 和 b 的正方形。
3. 此証畢氐定理。

4. 兩直邊正方形切片砌出斜邊正方形

數學家們梗係好鍾意去証明呢條定理，Cut the Knot 網站有成 122 個証明。

「有圖有真相」，本篇的動圖(GIF)，有助大家理解這條定理。

同畢氏定理最相關的事實，必然是其中一個直角三⻆形靚比例: 3-4-5，原因正正就是:
   3² + 4²  (兩個小直邊正方形面積)
= 9 + 16
= 25
= 5²   (等於大斜邊正方形面積)

原貼時間: 2013 Jan

最後更新: 2018 July

課題: Pythagoras' Theorem(畢氏定理) [中二]

來源: Pythagoras in 60 Seconds (Youtube)

相關文章：
【數字人生】從黃金寶出戰奧運談算術
【好文分享】玩21點拿著13點，莊家10點，要不要補牌呀？
唔識計數會使你損失11.7萬元 (When not knowing Math can cost you US$15,000 )
[老師不教的數學] 圓周界為何是「直徑×π」? 圓周率是什麼? 看GIF動畫圖詳解 [初小可理解]