2018 May 8 : 最新「最難」票數: Q1-23 : Q6(10票), 16(17票), 17(7票), 21(7票)
Q24-45 : Q29(4票), 30(4票), 32(7票), 33(4票), 34(4票), 40(5票)
2018 Apr 27 : 1至10條 已加新做法，稍後會再加我認為深的問題。
2018 Apr 25 : 邊條最難投票(進行中)
Q1-23 最多人投票覺得 Q6(9票), 17(11票), 21(6票)難
Q24-45 最多人投票覺得 Q29(4票), 30(3票), 32(4票), 34(3票)難
呢年算深，頗多問題若不懂變通，便要花較多時間做。
答案
BDCAA DDCDB
DACBD ABBDB
CBBAD CCACA
CCDCB ADBBA
DACBA
有問題(或有好方法)請留言。
**謝謝 Eddy Tsang 對第17條的方法分享 (2018 Apr 16)
~~~ 2018 年經濟 MC 逐題解釋 ~~~
~~~ ~~~ ~~~ ~~~ ~~~ ~~~
拉至頁底看「邊條最難」統計結果 及參與投票 (網已斷)
Q1-23 詳細答案在下方 | Q24-45在此~~~ 題號下方標記意思 ~~~
*sub - 可代數試 | *mc - 有 MC片教(youtube)
*skl - 有特別MC技巧 | *fmla - 有計數機內置程式可用
*prg - 有計數機程式可用 | *cal - 有等別計數機用法
~~~ ~~~
1. B
5*技巧 : 記住畢氏定理靚比例: 3-4-5; 5-12-13; 8-15-172. D
3. C *skl
Q3 另類方法 - Expand Term by Term(逐項展開)
可通過對比 Coefficient of Like Terms (同類項的系數) 去試答案，步驟如下:
可通過對比 Coefficient of Like Terms (同類項的系數) 去試答案，步驟如下:
- 先睇 "題目" 最尾 term "−12k" (頭尾 terms 最易睇，因最少 terms 乘埋組成)
- 應由 "答案選項" 兩個因式的尾 term "±2k, ±6"相乘組成，但皆為「正負得負」全部均為得"−12k"[未能篩走答案]
- 再睇 "題目" 的 3rd term "−4k²" ，應由 "答案選項" 兩個因式的 2nd term "±2k"相乘組成，只有 B, C 為「正負得負」得"−4k²" [篩走 A, D]
- 再睇"題目" 的 2nd term "−6h" ，應由 "答案選項" 第一因式的 1st term "h" 及 第二因式的 last term "±6" 相乘組成，答案 B, C 中只有 C 為「正負得負」得"−6h" [篩走 B, ∴答案為 C]
此題另類方法一般較慢，因要逐一試答案，數學稍差同學未能因式化時啱用
4. A *sub
Q4 另類方法 - Subsitution(代數)
代 x 為某實數 (Sub x = ?) 去試答案，步驟如下:
代 x 為某實數 (Sub x = ?) 去試答案，步驟如下:
- Sub x = 0，
(代 x = 0 時, 答案 C, D 分子為 '0', 非 '2') [篩走 C, D]
- 觀察到答案 A, B 分子皆為 14，所以把 代數 得出的答案擴分：
- (代x = 0 時, 答案 B 分母為 '−49', 非 '2') [篩走 B, ∴答案為 A]
此題代數法較快*，數學稍差同學另類方法更快、更保險*但有時代錯數(e.g.,7/3)會出錯 (多個答案/undefined)
5. A *skl *fmla (先試較易的答案先)
- 重寫方程為 standard form (標準式): y = −(x – 6)² + 16
- 只可以試答案 (問你邊個答案啱或錯一般只可逐個答案試)
- A. Cut x-軸，即有 root(s)，要 (1) Solve 或 (2) 計 Δ (determinant, 判別式)，需時較長，可先試答案 B, C, D。 [A 計 Δ 或 Solve 見下方]
- B. 錯（因 a 為負，曲線向下 [
] ） - C. 錯（Put x = 0, y = -20）
- D. 錯（Put x = 0, y ≠ 0）
⇒ 計數機[FMLA01] (-1, 12, -20) 可計計出 2 個答案 2 & 10，有 roots，A 啱
或
(2) 計 Δ:
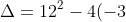(-20)%3D64%3E0 "\Delta =12^{2}-4(-3)(-20)=64>0")
所以有 2 個 roots，A 啱
6. D *skl [5* 技巧 - 目標為本]
做法略述:
1) 先快速望 選項 I, II, III 關係到什麼 variables (變數) 及數字
2) 再與兩條直線方程的 Slope, intercepts (斜率, 截距) 組成對比
3) [唔夠先再睇埋相交點，因較難搵]
(I) 關係到 a, c, 3 :
⟹ 涉及兩方程的 A 及 B*，所以要對比它們的 Slope^
*(Ax + By + C = 0) ^要注意不等式乘負數大於符號要轉向喔
)}\\&space;3&%3Eac\;&space;\;&space;\;&space;\;&space;\mathbf{{\color{Red}(\because&space;a%3C0^{**})}}&space;\end{align*} "2018 DSE Math MC Q6(2)")
∴ (I) 啱
**要 check a 的正負:
∵ L₁ 的 Slope 為正值 (左往右向上斜)
∴ -3/a > 0 ⟹ a < 0
(II) 關係到 a, b, d :
⟹ 涉及兩方程的 B 及 C，所以要 Put x = 0，對比它們的 y-intercepts
}&space;\end{align*})
∴ (II) 錯
(III) 關係到 3, b, c, d :
⟹ 涉及兩方程的 A 及 C，所以要 Put x = 0，對比它們的 y-intercepts
}&space;\end{align*})
∴ (III) 啱
7. D
&=3(2m-1)%5E%7B2%7D-2(2m-1)+1%5C%5C&space;&=12m%5E%7B2%7D-12m+3-4m+2+1%5C%5C&space;&=12m%5E%7B2%7D-16m+6&space;%5Cend%7Balign*%7D "\begin{align*} f(2m-1)&=3(2m-1)^{2}-2(2m-1)+1\\ &=12m^{2}-12m+3-4m+2+1\\ &=12m^{2}-16m+6 \end{align*}")
8. C *sub
**因上一步驟計得 a + b = -1，所以要 +a 去併出一個 a + b (+a −a 使方程不變)
所以有 2 個 roots，A 啱
6. D *skl [5* 技巧 - 目標為本]
做法略述:
1) 先快速望 選項 I, II, III 關係到什麼 variables (變數) 及數字
2) 再與兩條直線方程的 Slope, intercepts (斜率, 截距) 組成對比
3) [唔夠先再睇埋相交點，因較難搵]
(I) 關係到 a, c, 3 :
⟹ 涉及兩方程的 A 及 B*，所以要對比它們的 Slope^
*(Ax + By + C = 0) ^要注意不等式乘負數大於符號要轉向喔
**要 check a 的正負:
∵ L₁ 的 Slope 為正值 (左往右向上斜)
∴ -3/a > 0 ⟹ a < 0
(II) 關係到 a, b, d :
⟹ 涉及兩方程的 B 及 C，所以要 Put x = 0，對比它們的 y-intercepts
(III) 關係到 3, b, c, d :
⟹ 涉及兩方程的 A 及 C，所以要 Put x = 0，對比它們的 y-intercepts
7. D
8. C *sub
| g(1) = 1 + a + b | = 0 |
| a + b | = -1 |
| g(-1) | = 1 − a + b |
| = 1 − a + b + a − a ** | |
| = 1 − 2a + (a + b) | |
| = 1 − 2a + (-1) | |
| = -2a |
Q8 另類方法 - Subsitution(代數)
&=(-1)%5E%7B8%7D+(-1)%5E%7B7%7D+(-2)%5C%5C&space;&=-2%5C%5C&space;&=-2(1)%5C%5C&space;&=-2a&space;%5Cend%7Balign*%7D "\begin{align*} f(-1)&=(-1)^{8}+(-1)^{7}+(-2)\\ &=-2\\ &=-2(1)\\ &=-2a \end{align*}")
- 做法同上 (Factor theorem):
| g(1) = 1 + a + b | = 0 |
| a + b | = -1 |
- 代 a 為 1，b 為 -2 或其他 a + b = -1 的組合，
- 再用 Factor theorem :
此題代數法較慢，諗唔到 "+a −a" 的同學啱用
9. D
10. B
11. D
（解釋：k 若為 constant，如 5，k2＝25 亦是 constant）
12. A *sub
an+2 = an + an+1 意即任何數為前兩數之和：
Method 1：試數（應該最快）
∴ 8 是答案
Method 2：列式做：設 a1, a2 為 a 及 b
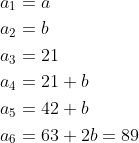
&=21%5C%5C&space;a&=8%5C%5C&space;%5Cend%7Balign*%7D "\begin{align*} 63+2b&=89\\ b&=13\\ a+(13)&=21\\ a&=8\\ \end{align*}")
13. C
14. B
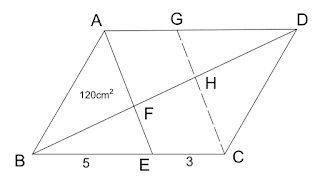
要用大減細，唔好當 AH 同 ED 都係 2 cm (因無實際量度 (measure) 過)
最大 area：6.5 × 4.5 − 1.5 × 1.5 = 27
最細 area：5.5 × 3.5 − 2.5 × 2.5 = 13
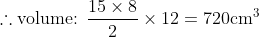
加虛線 GC 如圖
 "2018 DSE Math MC Q16")
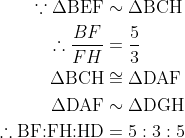
%5E%7B2%7D-5%5E%7B2%7D%7D%7B(5+3)%5E%7B2%7D%7D%5C%5C&=192%5Ctimes%5Cfrac%7B39%7D%7B64%7D%5C%5C&space;&=117%5C%5C&space;%5Ctherefore%5Csquare%5Ctextup%7BCDFE%7D&=117+120%5C%5C&space;&=237&space;%5Cend%7Balign*%7D "\begin{align*} \therefore \Delta \textup{BCH}&=120\times\frac{3+5}{5}\\&=192 \\ \therefore \square\textup{CEFH}&=192\times\frac{(5+3)^{2}-5^{2}}{(5+3)^{2}}\\&=192\times\frac{39}{64}\\ &=117\\ \therefore\square\textup{CDFE}&=117+120\\ &=237 \end{align*}")
Method 2 : 相似 Δ
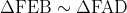
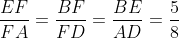
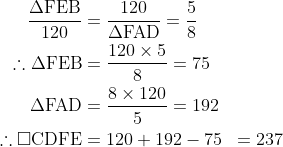
因為 a1 只可以是 8 或 13
| 試 8： | a1 | a2 | 21 | a4 | a5 | 89 |
| 8 | 13 | 21 | 34 | 55 | 89 | |
| ↑ | ↑ | ↑ | ||||
| 21-8 | 13+21 | 34+55 |
∴ 8 是答案
Method 2：列式做：設 a1, a2 為 a 及 b
13. C
14. B
要用大減細，唔好當 AH 同 ED 都係 2 cm (因無實際量度 (measure) 過)
最大 area：6.5 × 4.5 − 1.5 × 1.5 = 27
最細 area：5.5 × 3.5 − 2.5 × 2.5 = 13
15. D *skl
Pyth. Thm 計出橫切面Δ 的另一直邊為 15
Pyth. Thm 計出橫切面Δ 的另一直邊為 15
5*技巧 : 記住畢氏定理靚比例: 3-4-5; 5-12-13; 8-15-17
16. A
Method 1: 比三角面積（三角形同高比底 etc）加虛線 GC 如圖
17. B *skl *sub *prg
%5Cdiv2%3D24%5C%5C&space;DO&=30&space;%5Cend%7Balign*%7D "\begin{align*} DE&=(39+9)\div2=24\\ DO&=30 \end{align*}")
➀
%5E%7B2%7D%5Ctimes&space;%5Cfrac%7B106.26%7D%7B360%7D%5C%5C&space;&=265%5Cpi&space;%5Cend%7Balign*%7D "\begin{align*} \textup{Area of sector OABCD:}\\ \textup{[Prg3] Find }\angle \textup{AOD}&=106.26^{\circ}\\ or\\ \tan\theta=\frac{24}{18}&\Rightarrow \theta=53.13^{\circ}\\ &\Rightarrow 2\theta =106.26^{\circ}\\ \textup{Area of whole sector}&=\pi (30)^{2}\times \frac{106.26}{360}\\ &=265\pi \end{align*}")
➁ 再睇考卷圖 EF : FA 為 15 : 9 但明顯考卷不對，若跟 15 : 9 畫 sector OBC 應會略超過 1/4
265π / 4 = 66.25 π 所以答案應選 75 π
Alternative method
%5E%7B2%7D%5Ctimes&space;%5Cfrac%7B30%7D%7B360%7D%5C%5C&space;&=75%5Cpi&space;%5Cend%7Balign*%7D "\begin{align*} \textup{Let x = EG, y = OG}\\ \Delta \textup{OEG}&\sim \Delta \textup{BFG}\\ \frac{x}{y}&=\frac{15-x}{30-y}\\ 30x-xy&=15y-xy\\ \frac{x}{y}&=\frac{1}{2}\\ \therefore \angle \textup{BOC}&=30^{\circ}\\ \therefore \textup{Area}&=\pi (30)^{2}\times \frac{30}{360}\\ &=75\pi \end{align*}")
5*技巧 : 18，24，30 組成 3-4-5 畢氏定理靚比例＊再計應比較深，見 4 個答案差頗遠，可試數
➀
➁ 再睇考卷圖 EF : FA 為 15 : 9 但明顯考卷不對，若跟 15 : 9 畫 sector OBC 應會略超過 1/4
265π / 4 = 66.25 π 所以答案應選 75 π
Alternative method
18. B
%5Cdiv&space;2=104%5E%7B%5Ccirc%7D%5C%5C&space;%5Ctherefore&space;%5CDelta&space;%5Ctextup%7BBEC%7D&=180%5E%7B%5Ccirc%7D-110%5E%7B%5Ccirc%7D%3D76%5E%7B%5Ccirc%7D&space;%5Cend%7Balign*%7D "\begin{align*} \square \textup{AECF is a kite,}\\ \therefore \Delta \textup{AEC}&=(360^{\circ}-42^{\circ}-120^{\circ})\div 2=104^{\circ}\\ \therefore \Delta \textup{BEC}&=180^{\circ}-110^{\circ}=76^{\circ} \end{align*}")
19. D
(I) 啱：
%5Cdiv&space;2%5C%5C&space;&=36%5E%7B%5Ccirc%7D%5C%5C&space;%5Cangle&space;%5Ctextup%7BCDF%7D&=108%5E%7B%5Ccirc%7D-36%5E%7B%5Ccirc%7D%5C%5C&space;&=72%5E%7B%5Ccirc%7D%5C%5C&space;%5Ctherefore%5Cangle&space;%5Ctextup%7BCFD%7D&=180%5E%7B%5Ccirc%7D-72%5E%7B%5Ccirc%7D-36%5E%7B%5Ccirc%7D%5C%5C&space;&=72%5E%7B%5Ccirc%7D%5C%5C&space;%5Ctherefore&space;CD&=CF&space;%5Cend%7Balign*%7D "\begin{align*} \textup{int.}\angle \textup{ of regular pentagon:}\\ 180^{\circ}-\frac{360^{\circ}}{5}&=108^{\circ}\\ \therefore \angle \textup{DCF}&=(180^{\circ}-108^{\circ})\div 2\\ &=36^{\circ}\\ \angle \textup{CDF}&=108^{\circ}-36^{\circ}\\ &=72^{\circ}\\ \therefore\angle \textup{CFD}&=180^{\circ}-72^{\circ}-36^{\circ}\\ &=72^{\circ}\\ \therefore CD&=CF \end{align*}")
(II) 啱：
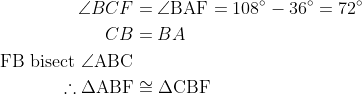
(III) 啱：
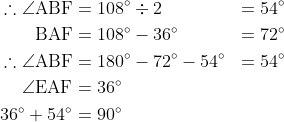
(III) 啱：
20. B *skl
Δ BEF ∼ Δ CDF ⇒ Δ CDF 亦為 3-4-5 比例
∵ CD = BF + CF
∴ Δ CDF 比例應為 3-4-5 的 3 倍：9-12-15
（∵ 9 + 3 = 12 才是正方形邊長）
∴ DF = 15
Alternative method
設 CF 和 CD 為 3k 和 4k
4k = 3k + 3
k = 3
∴ CF , CD 分別為 9 及 12
∴ DF = √ (9² + 12²) = 15 ( Pyth. Thm.)
5*技巧 : 用 3-4-5 諗Δ BEF 形成 3-4-5 靚畢氏定理比例
Δ BEF ∼ Δ CDF ⇒ Δ CDF 亦為 3-4-5 比例
∵ CD = BF + CF
∴ Δ CDF 比例應為 3-4-5 的 3 倍：9-12-15
（∵ 9 + 3 = 12 才是正方形邊長）
∴ DF = 15
Alternative method
設 CF 和 CD 為 3k 和 4k
4k = 3k + 3
k = 3
∴ CF , CD 分別為 9 及 12
∴ DF = √ (9² + 12²) = 15 ( Pyth. Thm.)
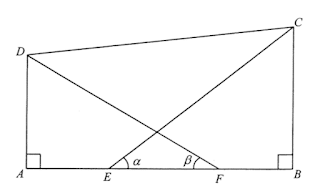
21. C
*sub
圖中明顯 2 角大小可不同
II 啱 ⇒
III 啱 ⇒
Alternative method
因為 AD 及 BC 高度冇定，可以設 α 及 β 分別為 45° 及 30° （或任何 2 個不同數值的角度），
另 AE = EF = FB 設為 1 cm （或其他相同的數），再計出 AD 及 BC，再 check I, II, III 是否正確。
22. B
∠DBE = ∠DEB = y (base ∠s. isos Δ)
∠CAD = ∠CBD = y (∠ in same seg.)
In Δ ABE,
66° + 30° + 3y = 180° (∠sum of Δ)
y = 28°
23. B
拮住中點，“ 1 ” 號格可轉至 2, 3, 4 號位而形狀完全重疊
∴ 4
Q24-45在此
2018 DSE Math MC 你覺得邊條最難?(Q1-23)
參與投票 |
若覺得這篇文章好，"分享" 給朋友吧！或留個 "Thank You" 呀！
想收到最新文章，可訂閱博客更新。 [keep updating: Q5 1)加 Eddy Q17 2)個別問題會再加一啲新做法]
Q17
回覆刪除EF = 15
Let x be a point on OC such that BX is perpendicular to OC.
Then BX =EF = 15
sin(BOC)=15/30
BOC = 30